Wykres pudełkowy (wykres skrzynkowy) służy do prezentacji wyników lub porównania danych. Zawiera informacje odnośnie położenia, rozproszenia i kształtu rozkładu danych. Ze względu na swoją kompleksowość (m.in. użycie ME, Q1, Q3) wykres pudełkowy jest często używany do porównania różnych rzeczy.
Są 2 główne warianty tworzenia wykresu pudełkowego:
- prostszy (bazujący na głównych statystykach)
- bardziej złożony (używany również do prezentacji wartości odstających, tzw. outlierów)
Ad1.
Do stworzenia prostego wykresu pudełkowego potrzebne jest nam 5 wartości:
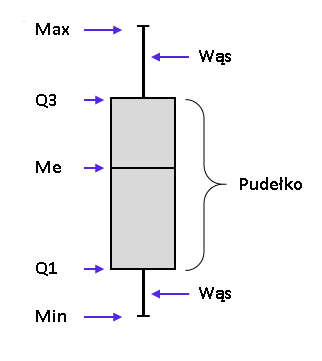
Max – wartość maksymalna
Q3 – trzeci kwartyl
Me – mediana
Q1 – pierwszy kwartyl
Min – wartość minimalna
Wąs: kreska łącząca wartość Min/Max z końcem pudełka.
Ważne informacje dotyczące 1. wariantu wykresu pudełkowego:
- Długość pudełka jest równa rozstępowi ćwiartkowemu \( Q_{3} – Q_{1} \)
- Wąsy mogą być różnej długości- wszystko zależy od tego ile wynosi wartość maksymalna i minimalna
- Mediana nie musi leżeć na środku pudełka
Ad2.
Do stworzenia bardziej złożonego wykresu pudełkowego potrzebujemy:
Q3 – trzeci kwartyl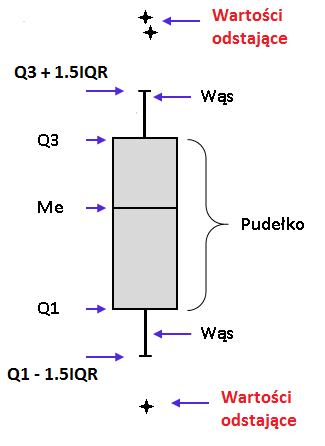
Me – mediana
Q1 – pierwszy kwartyl
IQR – roztęp ćwiartkowy
(przedział międzykwartylowy),
który jest wyliczany następująco:
IQR = Q3 – Q1
Wąsy wyznaczamy w następujący sposób:
dolny wąs \(= Q1 – 1.5 \cdot IQR \)
górny wąs \(= Q3 + 1.5 \cdot IQR \)
Jeżeli jakieś wartości są poniżej dolnego wąsa lub powyżej górnego wąsa wtedy nanosimy je na wykres jako gwiazdki. Te wartości reprezentują wartości odstające, czyli znacząco odbiegające od reszty.
Ważne informacje dotyczące 2. wariantu wykresu pudełkowego:
- Długość pudełka jest równa rozstępowi ćwiartkowemu \( Q_{3} – Q_{1} \)
- Wąsy są tej samej długości
- Mediana nie musi leżeć na środku pudełka
- Wykres służy również do znajdowania wartości odstających, które w sposób znaczący mogą zaburzać interpretację
Analiza wykresu pudełkowego:
- Położenie: o położeniu świadczy cały wykres pudełkowy m.in możemy określić zakres danych (Min, Max).
- Rozproszenie: im dłuższy wykres tym dane są bardziej rozproszone tzn. mogą przyjmować bardziej różniące się wartości. O rozproszeniu świadczą także długie wąsy – tzn. występują obserwacje skrajne (bardzo odbiegające od pudełka).
- Kształt: jeżeli wykres wygląda symetrycznie względem kreski z medianą to możemy podejrzewać że wykres cechy jest symetryczny. Jeżeli pudełko nie jest równo podzielone albo/i wąsy są różnej długości to mamy do czynienia z rozkładem asymetrycznym – najczęściej to czy asymetria jest prawostronna czy lewostronna możemy odczytać po odległości Max i Min od Mediany: jeżeli jedna z tych odległości jest znacząco większa to mamy asymetrię prawostronną(jeżeli znacząco większa jest odległość Max od Me) lub lewostronną(jeżeli odległość Min od Me jest większa).
Przykłady asymetrii można znaleźć tutaj.
A jeśli sa dane odstające to wtedy one wyznaczają maksimum i minimum czy dalej końce wąsów?
W zależności od przyjętej definicji: albo wąsy wyznaczają max i min, albo wartości mocno odstające są reprezentowane przez gwiazdki.
Dodałem drugą definicję wykresu pudełkowego.
“Jeżeli jakieś wartości są poniżej Min lub powyżej Max wtedy nanosimy je na wykres jako gwiazdki. Te wartości reprezentują wartości odstające, czyli znacząco odbiegające od reszty.”
Jak wartość z próby statystycznej może być poniżej Min, albo powyżej Max?
Jeśli jakaś wartość leży poniżej Q1-1,5IQR to jest podejrzana o nietypowość, jeśli poniżej Q1-3IQR to jest nietypowa dla próby. Analogicznie z Q3 tylko ze znakami + dla wartości IQR.
Pozdrawiam
Jak widać mogą:) Chodziło mi o min i max pudełka, czyli o dolny wąs i górny wąs.
Przepraszam za zamieszanie i już poprawiam by było bardziej oczywiste.
Jeżeli chodzi o wartości nietypowe to tutaj sprawa nie jest tak oczywista. Na angielskiej Wikipedii jest napisane, że wszystkie dane poza wąsami są uznawane za wartości odstające i tym się kierowałem w tym poście. Natomiast sposobów na wyznaczenie wąsów jest tam aż 5. Na stronie przedstawiłem 2, ponieważ z nimi spotkałem się w zadaniach, które mieli moi uczniowie.
Ty, zaprezentowałeś inny sposób na wyznaczenie wartości nietypowych. Tak na prawdę wszystko zależy od wykładowcy lub przyjętego sposobu na rozwiązywanie problemu.
Czy wykres drugiego typu nie powinien mieć wąsów o długości 1,5 większej od wysokości całego pudełka? Na obrazku są kilka razy mniejsze.
Zgadza się. Wykres jest czysto poglądowy.
Długość “wąsa wynosi” 1.5IQR tak jak zostało zaznaczone na obrazku.