Rozkład chi2 (chi kwadrat) jest rozkładem zmiennej losowej powstałym z rozkładu normalnego w poniższy sposób:
Niech \( X_{i} \sim N(0,1) \) dla i = 1, 2, … k będą zmiennymi niezależnymi wtedy zmienna rozkładu chi kwadrat o k stopniach swobody \( \Large \chi^{2}_{k} \) wyraża się wzorem:
\( \chi^{2}_{k} = \sum\limits_{i=1}^k X^{2}_{i}\)
Wykres rozkładu chi kwadrat
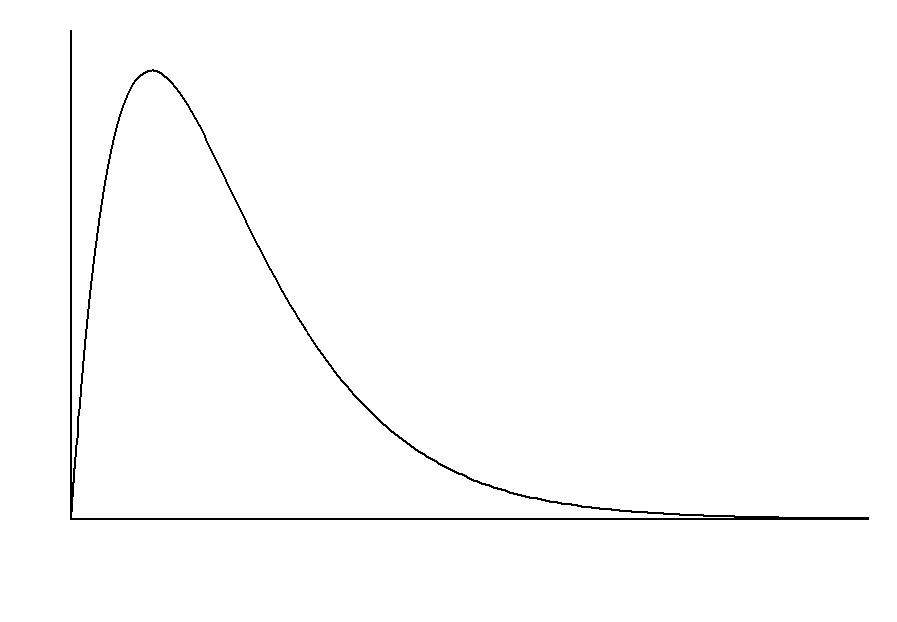 Cechy rozkładu Chi2
Cechy rozkładu Chi2
Z rysunku widać, że rozkład chi kwadrat jest rozkładem nieujemnym, o asymetrii prawostronnej (dłuższy prawy ogon rozkładu). Im większe k tym wykres jest bardziej spłaszczony i dłuższy- ogon rozkładu “wolniej opada”.
Gdzie wykorzystywany jest rozkład chi2?
Rozkład chi2 wykorzystywany jest przy analizie wariancji ( m.in. do wyliczenia prawdopodobieństwa, że wariancja spełnia jakiś warunek, przy wyznaczaniu poziomu ufności dla wariacji lub przy testowaniu hipotez dla wariancji) oraz przy testach m.in. test zgodności lub test niezależności.
Zadanie 1
Zmienna \( \chi_{25}^{2} \) ma rozkład Chi kwadrat z 25 stopniami swobody.
Znajdź takie t że:
1. \( F(t) = 0.95\)
2. \( F(t) = 0.1\)
3. \(1- F(t) = 0.1\)
4. \(1- F(t) = 0.01\)
Gdzie F jest dystrybuantą tego rozkładu.
Zadanie 2
Zmienna \( \chi^{2} \) ma rozkład Chi kwadrat z 18 stopniami swobody. Wyznacz:
- \( P(8.23 \leq \chi_{18}^{2} \leq 37.16) \)
- \( P(6.26 \leq \chi_{18}^{2} \leq 31.53) \)
w sumie powinno być do indeksu n, nie k.
Dzięki, już poprawione.
Mam pytanie, zad2 ad. 1
Skad wziela sie wartość
1-0,005=0,995
1-0.975=0,025
Dodałem wyjaśnienie do rozwiązania.