Aby dowiedzieć się więcej o medianie/dominancie kliknij w odpowiednie hasło: mediana , dominanta

Graficzne przedstawienie mediany i dominanty jest o wiele prostsze niż ich analityczne wyznaczenie, więc nie ma się czego obawiać.

Jedyne co będzie nam potrzebne do graficznego wyznaczania mediany i dominanty to szereg przedziałowy. Przedstawię rozwiązanie tylko dla szeregu przedziałowego ilościowego, ale zrobię odpowiednią adnotację jak to by wyglądało w szeregu przedziałowym z częstościami. \(\)

Dane:

Wartość \( X_{i} \)	Liczba\( n_{i} \)
1000-3000	2
3000-5000	3
5000-7000	10
7000-9000	7
9000-11000	1

Graficzne wyznaczenie dominanty:

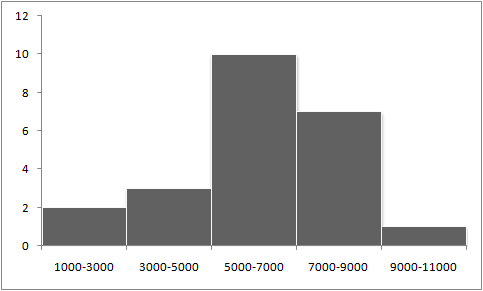
Będziemy potrzebowali histogram ilości:

Po pierwsze musimy określić, który przedział jest najliczniejszy (najczęstszy). Będzie to najwyższy przedział na wykresie. W naszym przykładzie takim przedziałem jest 5000-7000 i  to tam będzie dominanta.

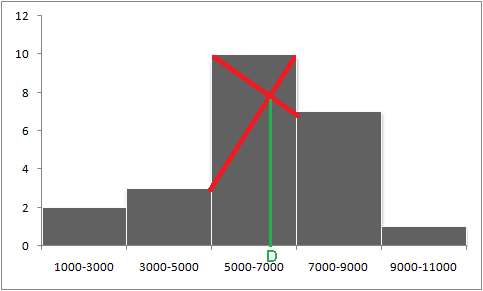
Następnie rysujemy 2 czerwone linie łączące górne krawędzie prostokąta zawierającego dominantę z przylegającymi górnymi krawędziami sąsiednich prostokątów.

Punkt przecięcia czerwonych linii wyznacza dominantę, która została zobrazowana zieloną linią między osią x, a punktem przecięcia.

Uwaga:

Jeżeli mamy 2 równoliczne (takie same \( n_{i} \) lub \( \omega_{i} \)) to nie istnieje Dominanta więc nie możemy jej też wyznaczyć graficznie.

Adnotacja do graficznego wyznaczania dominanty w szeregu przedziałowym z podanymi częstościami

Wszystko by wyglądało tak samo z tym, że zamiast ilości \( n_{i} \) na pionowej osi mielibyśmy częstości \( \omega_{i} \).

 

Graficzne wyznaczenie mediany:

Najpierw wyliczymy ilość skumulowane \( n_{isk} \).
Sposób wyliczenia został przedstawiony w kolumnie (Ilość skumulowana \( n_{isk} \)):

Wartość \( X_{i} \)	Ilość \( n_{i} \)	Ilość skumulowana \( n_{isk} \)
1000-3000	2	2
3000-5000	3	2 + 3 = 5
5000-7000	10	2 + 3 + 10 = 15
7000-9000	7	2 + 3 + 10 + 7 = 22
9000-11000	1	2 + 3 + 10 + 7 + 1 = 23

Będziemy potrzebowali jeszcze histogram ilości skumulowanej:

Tak samo jak w przypadku dominanty będziemy potrzebowali dorysować kilka linii.

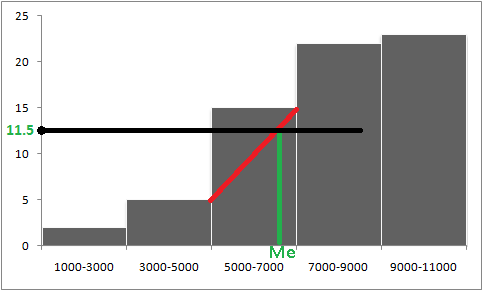
Zaczynamy od narysowania czarnej linii, która jest wyznaczona przed \( \frac{n}{2} \) i prowadzimy ją do momentu aż przejdzie przez prostokąt histogramu. W naszym wypadku jest to prostokąt odpowiadający 5000-7000, tzn. że w tym przedziale jest mediana.

Następnie rysujemy czerwoną linię, która łączy 2 punkty w których prostokąt z medianą styka się z sąsiednimi prostokątami.

Punkt przecięcia czarnej i czerwonej linii wyznacza medianę, która została zobrazowana zieloną linią między osią x, a punktem przecięcia.

 

Adnotacja do graficznego wyznaczania mediany w szeregu przedziałowym z podanymi częstościami

Wszystko by wyglądało tak samo z tym, że zamiast ilości skumulowanych na pionowej osi mielibyśmy częstości skumulowane. Zamiast zaznaczać \( \frac{n}{2} \) zaznaczamy 0.5.