Typowy przedział zmienności mówi nam o tym jakie wartości może przyjmować typowa cecha.
Wzory na typowy przedział zmienności:
- klasyczny: \( X_{typ} \in (\overline{X} – s, \overline{X} + s) \)
\(\overline{X}\) – średnia
s- odchylenie standardowe - pozycyjny: \( X_{typ} \in (Me – Q, Me + Q) \)
Me- mediana
Q- odchylenie ćwiartkowe
Dla przypomnienia odchylenie ćwiartkowe wyraża się wzorem
\( Q = \frac{Q_{3}- Q_{1}}{2} \)
gdzie \( Q_{1}, Q_{3} \) to odpowiednio 1szy i 3ci kwartyl rozkładu
Co oznacza typowy przedział zmienności?
Typowy przedział zmienności oznacza, że zawiera się w nim 67% wszystkich obserwacji
( \( \frac{2}{3} \) obserwacji )
Przeanalizujmy to na przykładzie:
Załóżmy, że interesują nas zarobki brutto w Polsce. Poniżej zarobki przedstawione są graficznie:
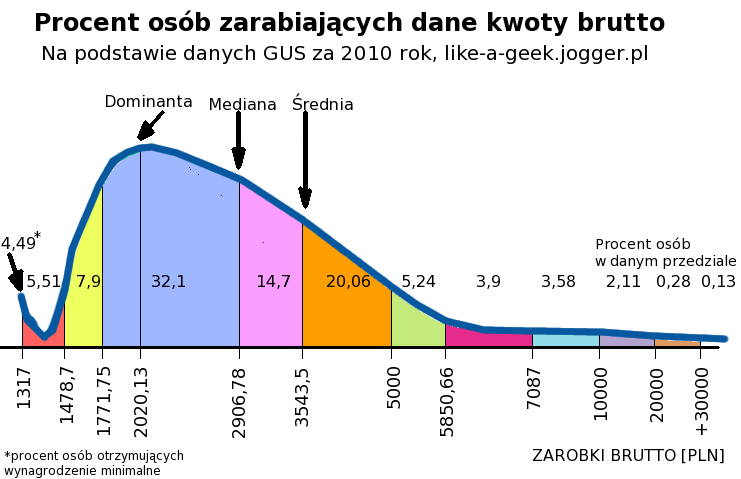 Średnia wynosi około 3.5 tyś. zł. Zastanówmy się czy coś nam powie, że zarobki w Polsce zawierają się w przedziale od minimum płacowego do np. 100 tyś.?
Średnia wynosi około 3.5 tyś. zł. Zastanówmy się czy coś nam powie, że zarobki w Polsce zawierają się w przedziale od minimum płacowego do np. 100 tyś.?
NIC.
Dużo bardziej interesuje nas, że 67% osób w Polsce pracujących legalnie zarabia między 1.7tyś. a 5tyś. zł brutto.
Załóżmy teraz, że chcielibyśmy stworzyć kampanię reklamową dla naszego produktu- dużo łatwiej jest nam skonstruować treść reklamy dla osób zarabiających między 1.7 a 5 tyś. zł niż 1.3 i 100tyś. zł.