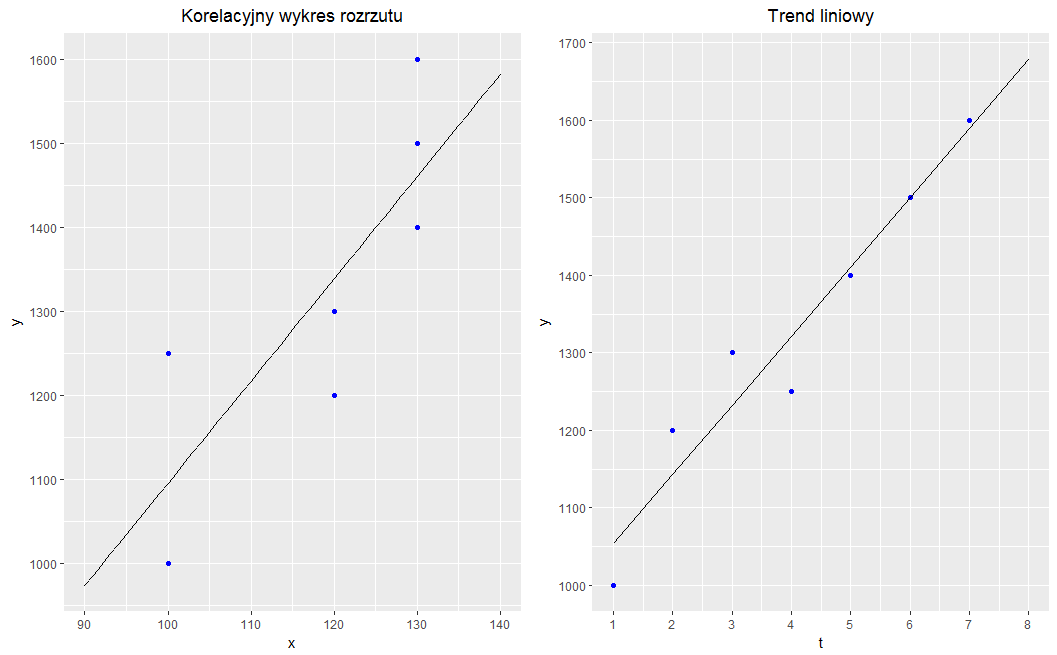
Trend liniowy jest specjalnym przypadkiem regresji liniowej gdzie zmienną objaśniającą X jest zmienna czasowa t.
W takim przypadku mówimy, że mamy do czynienia z szeregiem czasowym, czyli danymi, które są uszeregowane względem czasu.
Definicja: \(\)
Liniowa funkcja trendu jest dana wzorem
\( y = a \cdot t + b \)
a – współczynnik kierunkowy trendu: \( \large a = \frac{\sum ( t_{i}- \overline{X} ) \cdot( Y_{i}- \overline{Y} ) }{\sum ( t_{i}- \overline{t} )^{2}} \)
b – wyraz wolny trendu: \( \large b = \overline{Y} – a \cdot \overline{t} \)
\( t_{i} \), \( Y_{i} \) wartości zmiennych t i Y
\( \overline{t} \), \( \overline{Y} \) – średnie zmiennych t i Y
Gdy a > 0 to mamy do czynienia z rosnącym trendem. Im większe a tym wartość Y szybciej rośnie w czasie.
Gdy a < 0 to mamy do czynienia z malejącym trendem. Im mniejsze a tym wartość Y szybciej maleje w czasie.
Załóżmy, że mamy dane miesięczne zawierające wielkość sprzedaży oraz wydatki na reklamę:
| Miesiąc | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Sprzedaż [zł] | 1000 | 1200 | 1300 | 1250 | 1400 | 1500 | 1600 |
| Koszt reklamy [zł] | 100 | 120 | 120 | 100 | 130 | 130 | 130 |
Wtedy
W przypadku regresji liniowej pytamy: jaka będzie sprzedaż przy określonych wydatkach na reklamę. Chcąc oszacować wielkość sprzedaży w 9-tym miesiącu potrzebujemy wiedzieć jakie będą wydatki na reklamę.
W przypadku trendu liniowego pytamy: jak sprzedaż zmienia się w czasie. W tym przypadku nie potrzebujemy wiedzieć jakie będą wydatki na reklamę. Po prostu założymy, że trend się utrzyma i w kolejnym miesiącu również zanotujemy wzrost.
Gdy mamy zmienną objaśniającą (np. wydatki na reklamę) lepiej jest użyć regresji liniowej niż analizy trendu. Niestety nie zawsze mamy zmienną objaśniającą i w niektórych przypadkach możemy bazować tylko na trendzie.
Zadanie 1
Miesięczna wielkość sprzedaży została przedstawiona w tabeli
| Miesiąc | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Sprzedaż [zł] | 1000 | 1200 | 1300 | 1250 | 1400 | 1500 | 1600 |
1. Wyznacz liniową funkcje trendu i narysuj ją
2. Zinterpretuj współczynniki funkcji trendu
3. Zakładając, że trend utrzyma się oszacuj wartość sprzedaży w 10-tym miesiącu.
Zadanie 2
Liczba pasażerów lotniczych na świecie została przedstawiona w poniżej tabelce. Oszacuj liniowy trend w podanym okresie.
| Rok | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|---|
| L pasaż. [mld] | 1,97 | 2,072 | 2,209 | 2,208 | 2,250 | 2,628 | 2,787 | 2,894 | 3,048 | 3,227 |