Rozkład t-studenta – wprowadzenie

Rozkład t-studenta (nazywany również rozkład t albo rozkład studenta) to rozkład prawdopodobieństwa stosowany przy konstruowaniu przedziałów ufności, testowaniu hipotez statystycznych oraz do oceny błędu pomiaru.
Do wyznaczania wartości rozkładu używa się tablicy rozkładu t-studenta.

Kiedy używamy rozkładu t studenta? \(\)

Rozkład t studenta stosujemy tylko w sytuacji gdy odchylenie standardowe populacji jest nieznane, a rozmiar próby(ilość obserwacji) jest mniejsza niż 30. W przypadku gdy rozmiar próby jest większy lub równy 30 wtedy zamiast brać rozkład t bierzemy rozkład normalny. Wynika to z faktu, że rozkład t studenta dla \( n \geq 30 \) jest bardzo podobny do rozkładu normalnego. Dla n < 30 rozkład studenta jest „szerszy”, tzn. bardziej prawdopodobne są wartości mocno odbiegające od średniej niż w przypadku rozkładu normalnego.

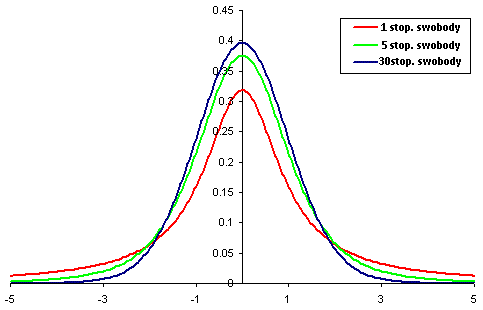
Przedstawienie rozkładu t studenta dla 1,5 i 30 stopni swobody
Przedstawienie rozkładu t studenta dla 1, 5 i 30 stopni swobody. Czerwona linia jest dużo bardziej rozległa niż niebieska.

 

Własności rozkładu t studenta

  • Rozkład t studenta używamy gdy nieznane jest odchylenie
    standardowe populacji oraz gdy próba jest niezbyt liczna (n < 30)
  • Dla \( n \geq 30 \) rozkład t studenta przybliżamy rozkładem normalnym N(0,1)
  • Rozkład t- studenta jest rozkładem symetrycznym
  • Rozkład studenta jest rozkładem jednomodalnym (ma jedną „górkę”)
  • Im mniej obserwacji tym rozkład jest szerszy

O co chodzi z odchyleniem standardowym populacji?

Jest to bardzo ważne pojęcie gdyż często jest ono zawarte przy konstruowaniu przedziałów ufności oraz przy testowaniu hipotez. Często w zadaniach mamy podane odchylenie standardowe jednak nie zawsze jest to odchylenie standardowe populacji. Aby w zadaniu odchylenie standardowe dotyczyło populacji musimy znać je bez danych. Jeżeli jest napisane, że rozkład wagi nakrętek w pewnej fabryce jest zmienną o odchyleniu standardowym 2 to oznacza to, że odchylenie standardowe populacji wynosi 2. Jeżeli natomiast byłoby napisane: wzięto 20 sztuk nakrętek i na podstawie ich wagi wyznaczono odchylenie standardowe równe 2.2 to dotyczy ono tylko tej grupy i nie jest to odchylenie standardowe populacji.

Zadania

W zadaniach będziemy korzystali z tablicy rozkładu t-studenta dostępnej tutaj

Zadanie 1

Zmienna losowa X ma rozkład t-studenta o 5 stopniach swobody. Oblicz:

  1. \( P(X < -0.559) \)
  2. \( P(-0.559 < X <0.559) \)

Dalsza część treści jest płatna. Dokonaj zakupu lub zaloguj się

Regulamin dostępny tutaj
Zaloguj się lub Wykup
Sprawdź Wykup
Anuluj
Dostęp do wszystkich treści - 30 dni, 109zł
Dostęp do wszystkich treści - 6 miesięcy, 129zł
Odblokuj dostęp do wszystkich treści na 30 dni
Sprawdź
Odblokuj dostepDokonując zamówienia potwierdzasz zapoznanie się z regulaminem
Odblokuj dostęp do wszystkich treści na 6 miesięcy
Sprawdź
Odblokuj dostepDokonując zamówienia potwierdzasz zapoznanie się z regulaminem
Anuluj

Zadanie 2

Zmienna losowa X ma rozkład t-studenta o 13 stopniach swobody. Oblicz:

  1. \( P(X > 0.694) \)
  2. \( P(X > -0.694) \)
  3. \( P(X \leq -1.771) \)

Treść dostępna po zalogowaniu

Zadanie 3

Zmienna losowa X ma rozkład t-studenta o 15 stopniach swobody. Znaleźć liczbę a, dla której:

  1. \( P(|X| > a) = 0.04 \)
  2. \( P(X > a) = 0.02 \)

Treść dostępna po zalogowaniu

Zadanie 4

Zmienna losowa X ma rozkład t-studenta o n stopniach swobody. Znajdź n jeżeli

  1. \( P(|X| > 1.134) = 0.3 \)
  2. \( P(X > 2.028) = 0.035 \)

Treść dostępna po zalogowaniu

Komentarze:

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.

This site uses Akismet to reduce spam. Learn how your comment data is processed.