Do czego służy dystrybuanta?
Czasem nie interesuje nas konkretne zdarzenie, a grupa zdarzeń, np. nie interesuje nas, jaka jest szansa, że na zakupach wydamy dokładnie 200zł, ale będzie nas interesowało jaka jest szansa, że wydamy mniej niż 200zł, inaczej byśmy weszli na debet a tego nie chcemy. Do wyliczenia takiego prawdopodobieństwa posłużmy się dystrybuantą, czyli prawdopodobieństwem, że zajdzie zdarzenie nie większe od ustalonej wartości (w powyższym przykładzie od 200zł).
Definicja dystrybuanty
\(\)
\( F_{X}(t) \) – Dystrybuanta rozkładu X w punkcie t to prawdopodobieństwo, że zajdzie zdarzenie mniejsze bądź równe t, tzn.
\( F_{X}(t) = P( X \leq t ) \)
Graficzne przedstawienie dystrybuanty:
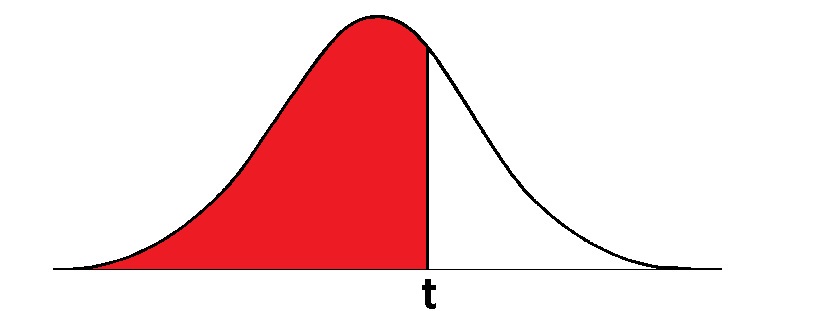
Na czerwono została zaznaczona wartość dystrybuanty w punkcie t dla rozkładu normalnego.
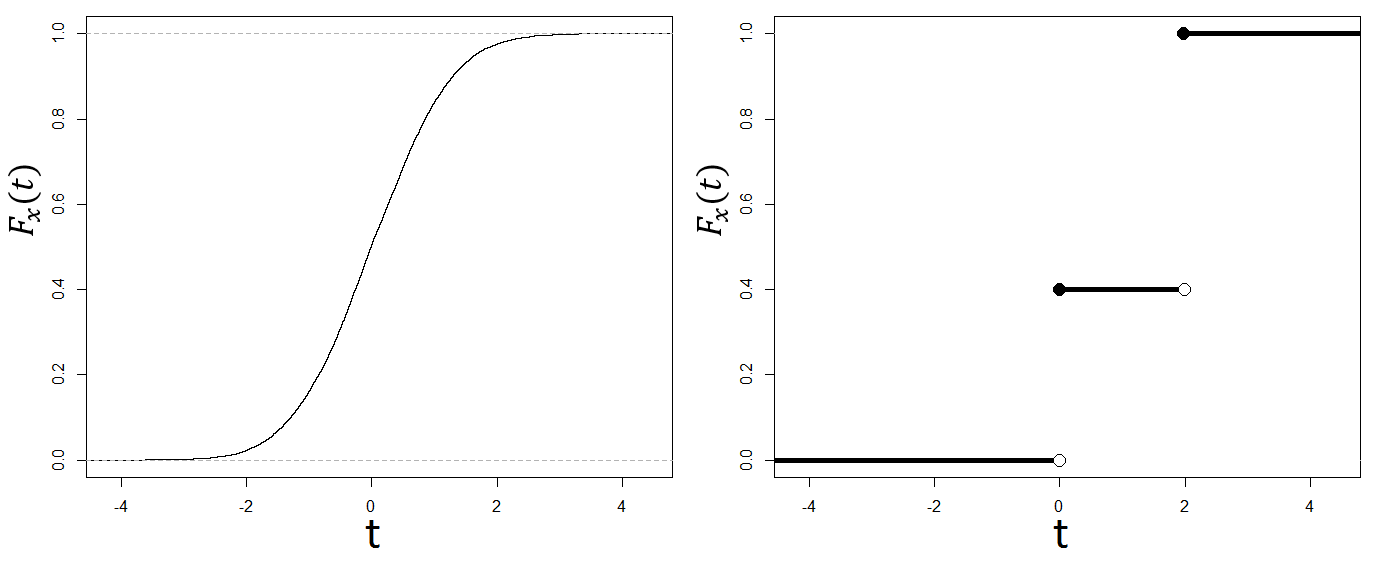
Poniżej zaprezentowano przykładowe wykresy dystrybuanty dla rozkładu ciągłego (po lewej) i rozkładu dyskretnego (po prawej)
Podstawowe własności dystrybuanty:
- \( F_{X}(t) \in [0,1] \) – dystrybuanta przyjmuje wartości z przedziału [0,1]. Jest to prosty fakt, wynikający z tego, że najmniejszą szansą na zajście zdarzenia jest 0 (0% – zdarzenie w ogóle nie zajdzie), a największą 1 (100% że zdarzenie na pewno zajdzie).
- \( F_{X}(t) \) – jest funkcją nie malejącą, czyli jeżeli weźmiemy 2 punkty \( t_{1} \) i \( t_{2} \) to jeżeli \( t_{1} < t_{2} \) to \( F_{X}(t_{1}) \leq F_{X}(t_{2}) \) – pisząc po ludzku: poruszając się w prawo wartość dystrybuanty nie będzie malała.
Przykład: Prawdopodobieństwo, że wydamy nie więcej niż 300zł jest większe niż tego, że wydamy nie więcej niż 200zł. - \( F_{X}(t) \)- prawostronnie ciągła, czyli jeżeli na wykresie wystąpi nieciągłość typu skok, to otwarta kropka będzie należeć do linii po lewej stronie, a zamalowana po prawej stronie
- \(\lim \limits_{t \to – \infty} F_{X}(t) = 0 \)
- \(\lim \limits_{t \to \infty} F_{X}(t) = 1 \)
Dystrybuanta empiryczna
Dystrybuanta empiryczna to dystrybuanta wyliczona wprost z danych. W takiej sytuacji nie znamy prawdziwego rozkładu i bazujemy tylko na dostępnych obserwacjach, np. przepytaliśmy 100 osób jaki jest ich wzrost i na tej podstawie określamy empiryczny rozkład oraz wyznaczamy empiryczną dystrybuantę.
Dystrybuanta teoretyczna
Z dystrybuantą teoretyczną mam do czynienia gdy znamy rozkład danego zjawiska. Wtedy nawet nie mając obserwacji możemy wyliczyć dystrybuantę (dlatego nazywamy ją dystrybuantą teoretyczną).
Dystrybuantę teoretyczną możemy wyznaczyć np.
- dla rzutu kostki ponieważ rozkład zmiennej jest znany ( \( P(X=k) = \frac{1}{6} \) dla \(k=1,2,3,4,5,6 \) )
- dla zdarzeń, które opisane są rozkładem normalnym N(0,1) (np. wynikające z centralnego twierdzenia granicznego)
Porównanie dystrybuanty empirycznej z dystrybuantą teoretyczną
Dystrybuanta empiryczna jest przybliżeniem dystrybuanty teoretycznej. Im więcej mamy obserwacji tym dystrybuanta empiryczna jest bliższa dystrybuancie teoretycznej co oznacza, że mając dużo danych* dystrybuanta empiryczna jest również dystrybuantą teoretyczną.
*o ile te dane są wybrane w sposób losowy.
Przykład dystrybuanty empirycznej i dystrybuanty teoretycznej
Rozważmy zdarzenie losowe: suma orłów w 10 rzutach symetryczną monetą.
Liczba orłów zawiera się między 0 a 10. Prawdopodobieństwo każdej wartości możemy wyliczyć korzystając z rozkładu dwumianowego. Mając wyliczone prawdopodobieństwo możemy narysować dystrybuantę teoretyczną – kolor niebieski.
Dodatkowo wykonaliśmy 20 serii rzutów (każdy po 10) i zliczyliśmy liczbę orłów w każdej serii. Następnie wyliczyliśmy rozkład empiryczny oraz dystrybuantę empiryczną – kolor czerwony.
Z racji małej liczby obserwacji (20) dystrybuanta empiryczna mocno odstaje od dystrybuanty teoretycznej. Dla n = 1000 różnica jest minimalna.

Jak wyliczyć dystrybuantę empiryczną?
Przykłady jak wyliczyć dystrybuantę empiryczną znajdują się w dziale z zadaniami.
Zadania z dystrybuanty – kliknij tutaj
Witam, Pańska strona jest przecudowna! Naprawdę wiele się z niej dowiedziałam,bo wszystko jest jasno napisane,co w przypadku matematyki rzadko się zdarza ;). Zwracam się z uprzejmą prośbą, aby pomógł mi Pan w rozwiązaniu następującego zagadnienia: określanie dystrybuanty,gdy mamy funkcję gęstości np. określ dystrybuantę dla funkcji F(x) = 2sinx dla 0<= x <= π/3 , w pozostałych przypadkach F(x) = 0. Z góry bardzo dziękuję :)
Bardzo przyjemnie wytłumaczone, dzięki!
Kolejny świetny wpis! Dziękuję za poświęcony czas! :)
Dziękuję:)
świetnie wytłumaczone, nareszcie załapałam o co chodzi, dzięki !!!
Jasno i zrozumiale, dziękuję za objaśnienie , świetna robota . Czytałem opis w Wikipedii ale tam opis był tylko częsciowo zrozumiały
Dzień przed egzaminem ze staty – mega ratunek :)
Piękne wyjaśnienie
obrazek niestety wprowadza w błąd…
podobno dystybuanta jest funkcją nie malejącą, czyli rosnącą lub stałą, a co widzimy na obrazku? Od pewnego momentu jest malejąca.
Na rysunku czarna linia oznacza rozkład prawdopodobieństwa i to może maleć. Natomiast dystrybuanta to pole pod wykresem, które zostało zaznaczone na czerwono. I wtedy wszystko się zgadza: zwiększając x, zwiększamy czerwone pole, czyli wartość dystrybuanty, czyli jest ona niemalejąca.
Z ciekawości, skoro dystrybuanta jest w gruncie rzeczy polem pod wykresem, to czy można by użyć całeczki?
Zgadza się. Dokładnie tak się matematycznie definiuje dystrybuantę, tj. jako całkę z prawdopodobieństwa od – nieskończoności do t.
Bardzo fajnie wytłumaczone!!!!!
No nareszcie! Obliczyć umiałam, ale jakby ktoś mnie zapytał czym jest dystrybuanta, to (do tej pory) usłyszałby tylko “yyyyy” ;)
Bardzo dziękuję!
To mi się podoba, w jasny sporób jak krowie na rowie…dlaczego wykładowcom brakuje tej jednej klepki odpowieadającej za proste tłumaczenie (pozornie) zawiłych kwestii.
Dziękuję bardzo za tak jasne przedstawienie zagadnienia, brakowało tego na innych stronach :)
“Poniżej zaprezentowano przykładowe wykresy dystrybuanty dla rozkładu ciągłego (po lewej) i rozkładu dyskretnego (po lewej)” – coś tu nie pasuje ;)
Dzięki poprawione :)
Dziękuję :)
Fajnie, że stracilem 4 godziny, by w końcu się upewnić, że cały ten artykuł jest błędny i wewnętrznie sprzeczny, treść i wykresy są niekonsystentne. Wg wszystkich innych źródeł:
F(t) = P(X < t)
Cały artykuł do przepisania na nowo. Aż dziw, że nikt tego tu wcześniej nie odkrył…
Cześć,
Sprawdziłem parę żródeł polskich i angielskich i JEDYNYM na którym głównym wzorem jest F(t) = P(X < t) jest pwn.pl Nie mniej nawet na nim jest adnotacja, żę: "czasem definiowana jako funkcja, która każdej liczbie rzeczywistej x przyporządkowuje prawdopodobieństwo P {X ≤ x}". Różnica z definicją F(t) = P(X < t) jest taka, że wtedy dystrybuanta będzie lewostronnie ciągła.
Świetny materiał, dziękuję!
Sprawdziłem również i dotarłem do zbieżnych informacji. Jednak różnic jest więcej. Np, konsekwencją odmiennej definicji jest to, że wykresy są nieciągłe po prawej stronie oraz przedziały są otwarte z lewej strony. Pozdrawiam
I prostuję – nie miałem racji. Artykuł jest konsekwentny w stosunku do obranej definicji. Przepraszam
Nic nie szkodzi. Pozdrawiam i życzę miłej nauki:)