Co to jest rozkład normalny?
Rozkład normalny, zwany również rozkładem Gaussa lub krzywą Gaussa, jest najważniejszym rozkładem statystycznym. Rozkład normalny jest też bardzo intuicyjny: większość obserwacji jest skupiona wokół średniej, obserwacje leżące dalej od średniej występują rzadziej. \(\)
Rozkład normalny przykład
Przeanalizujmy wzrost mężczyzn w Polsce. W/g danych z 2001 roku średni wzrost mężczyzn wynosi 177.4 cm. Większość obserwacji jest skupiona wokół tej wartości, tzn. że większość mężczyzn ma wzrost między 150cm a 200cm. Oczywiście zdarzają się mężczyźni o wzroście poniżej 150cm lub powyżej 200cm ale występują one stosunkowo rzadko- by się o tym przekonać wystarczy przejść się ulicą i sprawdzić jak często pojawią się mężczyźni ze wzrostem poniżej 150cm lub powyżej 200cm.
Rozkład normalny definicja
Rozkład normalny \( \large N(\mu, \sigma) \) ma 2 parametry:
- \( \mu \) oznacza wartość oczekiwaną, czyli średnią. Czasem zamiast \( \mu \) używa się literkę m.
- \( \large \sigma \) oznacza odchylenie standardowe- im większe odchylenie standardowe tym częściej występują obserwacje bardziej oddalone od średniej.
Czym jest krzywa Gaussa?
Krzywa Gaussa jest krzywą prezentującą rozkład
prawdopodobieństwa rozkładu \( \large N(\mu, \sigma) \):
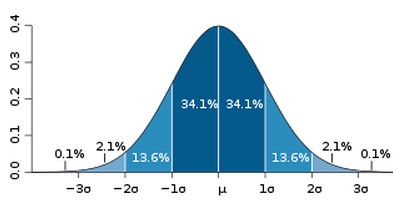
W okolicy wartości średniej(w odległości \( \large \sigma \)) znajduje się 68% obserwacji. W celu szczegółowej analizy wykresu Gaussa polecam wejść w temat Reguła (3 sigma ). Reguła ta definiuje jak dużo obserwacji znajduje się w określonej odległości od średniej.
Własności rozkładu normalnego
1. Rozkład normalny jest symetryczny względem średniej
2. Średnia równa się medianie i dominancie
3. Jeżeli do rozkładu normalnego dodamy liczbę (lub pomnożymy przez liczbę) to uzyskany rozkład też jest rozkładem normalnym:
\( X \sim N(\mu, \sigma) \) oraz a, b \( \in \mathbb{R} \) oraz \(\large b > 0 \) wtedy \( a+ bX \sim N(a + b \cdot \mu, b \sigma) \)
4. Suma rozkładów normalnych jest rozkładem normalnym:
Jeżeli \( X_{1} \sim N(\mu_{1}, \sigma_{1}) \), \( X_{2} \sim N(\mu_{2},\sigma_{2}) \) to \( X_{1}+X_{2} \sim N(\mu_{1} + \mu_{2}, \sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}}) \)
5. Średnia rozkładu normalnego jest rozkładem normalnym:
\( X \sim N(\mu, \sigma) \) to \( \overline{X} \sim N( \mu, \frac{\sigma}{\sqrt{n}} ) \)
6. W pewnych sytuacjach mając rozkład, który nie jest rozkładem normalnym, możemy go traktować jak rozkład normalny – więcej na stronie Centralne Twierdzenie Graniczne.
7. Jeżeli \( X_{i} \sim N(0,1) \) to \( \sum X_{i}^{2} \) jest z rozkładu Chi kwadrat z n-stopniami swobody – Chi2(n) – ten wniosek przyda nam się przy Teście Zgodności
Dowiedz się więcej o rozkładzie normalnym
Przed rozwiązaniem zadań z rozkładu normalnego warto przeczytać co to jest standaryzacja rozkładu normalnego oraz co to jest Centralne Twierdzenie Graniczne.
Zadania z rozkładu normalnego dostępne są tutaj:
Czym jest ten X?
X jest zmienną z rozkładu normalnego o podanych parametrach.
dzieki haha