Histogram jest najpopularniejszym sposobem przedstawienia rozkładu empirycznego cechy. Rozkład empiryczny oznacza rozkład otrzymany na podstawie danych – empiryczny, znaczy doświadczalny.
Interpretacja histogramu
Histogram służy do analizy zbiorowość, co oznacza, że jesteśmy w stanie odpowiedzieć m.in. na pytania:
- który przedział jest najliczniejszy (określenie dominanty)
- czy rozkład jest symetryczny czy może asymetryczny / skośny.
- czy występują przedziały mocno odstające od reszty
Histogram to graficznie przedstawiony szereg przedziałowy
Szereg przedziałowy składa się z przedziałów oraz liczby obserwacji, które się w nich znajdują. Bez histogramu ciężko byłoby zauważyć pewne rzeczy np. skośność. \(\)
Kiedy przydaje się histogram?
Histogram przydaje się gdy mamy dużo różnych obserwacji. Powiedzmy, że chcemy zbadać zarobki 2000 osób. Zarobki wielu osób różnią się jednak widzimy duże skupiska koło 2000zł, 2500zł i 3000zł. Dzięki histogramowi – który operuje na przedziałach – jesteśmy w stanie łatwo pogrupować i przeanalizować naszą zbiorowość.
Jak zbudować histogram ilościowy i częstościowy:
Histogram ilościowy przedstawia ilość obserwacji w każdym przedziale natomiast histogram częstościowy przedstawia częstość obserwacji w każdym przedziale (procent obserwacji znajdujący się w przedziale)
- Policz ile mamy obserwacji
Warto to zrobić na początku by potem nie zgubić jakiejś obserwacji przy liczeniu ile razy występuje każda obserwacja. - Uszereguj obserwacje
Ułatwi nam to liczenie ile obserwacji należy do danego przedziału - Określ k – liczbę przedziałów histogramu
\( k \approx \sqrt{n}\), gdzie n- ilość obserwacji - Określ h – długość każdego przedziału\( h = \frac{max-min}{k} \) gdzie max i min to odpowiednio wartości największa i najmniejsza
- Wyznacz przedziały
Przydziały są lewostronnie domknięte i prawostronnie otwarte, tzn : \( [Xp, Xk) \), \(X_{p} \) – początek przedziału, \( X_{k} \) – koniec przedziału. Poza ostatnim który musi być domknięty również z prawej strony aby “złapać” wartość największą. Koniec jednego przedziału jest początkiem drugiego przedziału- tak by była zachowana ciągłość. - Policz ile obserwacji wpada do każdego przedziału i sprawdź czy liczności sumują się do n!
Sumujemy w celu uniknięcia błędu- w tym momencie mamy skonstruowany histogram ilości. W celu skonstruowania histogramu częstości należy wykonać punkt 7 - Histogram częstości : \(n_{i} \) zamień na \( \omega_{i} = \frac{n_{i}}{n} \)
Po wykonaniu wyżej wymienionych kroków należy jeszcze narysować histogram.
Przykład tworzenia histogramu
Zarobki w pewnej firmie przedstawiają się następująco:
2000, 2010, 2020, 2015, 2500, 3000, 2500, 2450, 2060, 2700, 2840, 2550, 2340, 2900, 3000, 2250, 2300, 3000, 2990, 2600.
Skonstruuj histogram płac pracowników oraz zinterpretuj wyniki.
- n = 20
- Uszeregowane obserwacje:
2000, 2010, 2015, 2020, 2060, 2250, 2300, 2340, 2450, 2500, 2500, 2550, 2600, 2700, 2840, 2900, 2990, 3000, 3000, 3000 - Liczba przedziałów:
\( k = \sqrt{20} \approx 4 \) - Długość przedziałów:
\( h = \frac{3000-2000}{4} = 250 \) - Przedziały:
\( [2000, 2250) \), \( [2250, 2500) \), \( [2500, 2750) \), \( [2750, 3000] \) - Ile obserwacji wpada do każdego przedziału:
PRZEDZIAŁ ILOŚCI \( n_{i} \) \( [2000, 2250) \) 5 \( [2250, 2500) \) 4 \( [2500, 2750) \) 5 \( [2750, 3000] \) 6
- Jak często obserwacje wpadają do każdego przedziału:
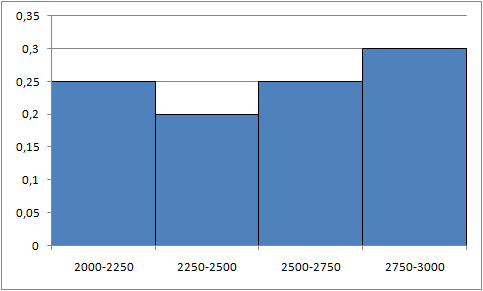
PRZEDZIAŁ CZĘSTOŚCI \( \omega_{i} \) \( [2000, 2250) \) \( \frac{5}{20} = 0.25\) \( [2250, 2500) \) 0.2 \( [2500, 2750) \) 0.25 \( [2750, 3000] \) 0.3
Histogramy zostały wyznaczone. Teraz pozostaje tylko je narysować i zinterpretować:
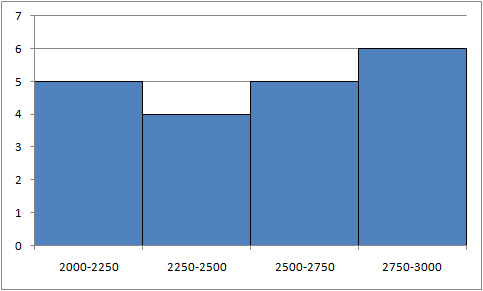
Histogram ilościowy
Histogram częstościowy
Interpretacja histogramu:
- Zarobki pracowników mieszczą się między 2000zł a 3000zł
- Obserwacje są rozłożone równomiernie na przedziały co oznacza, że zarobki pracowników są zróżnicowane (brak jednego dominującego przedziału)
- Najliczniejszym przedziałem jest przedział \( [2750, 3000] \) co oznacza, że w tym przedziale jest dominanta.
- Na podstawie histogramu nie zaobserwowaliśmy asymetrii (skośności) rozkładu
Mamo, ratunku!
świetnie wytłumaczone wielki +++++++++
no supcio
Krotko, sensownie i na temat, dzieki wielkie!
Wszystko bardzo dobrze wytłumaczone, dziękuję.
Lepiej się nie da wytłumaczyć. Pozdrawiam.