Wszystkie zadania dot. rozkładu normalnego w których należy policzyć prawdopodobieństwo sprowadzają się tak naprawdę do kilku przypadków, które tutaj omówimy. Do każdego przypadku będzie dołączony rysunek ilustrujący podane prawdopodobieństwo oraz wzór. Na kolokwium wystarczy pamiętać wzór jednak w stresie można zapomnieć wzoru więc warto przeanalizować obrazki i wyrobić sobie intuicję dotyczącą rozkładu normalnego.

Wzory:
\( P(X \leq t) = \begin{cases} \Phi(t) & t \geq 0 \\ 1- \Phi(-t) & t < 0 \end{cases} \)

\( P(X \geq t) = \begin{cases} 1 – \Phi(t) & t \geq 0 \\ \Phi(-t) & t < 0 \end{cases} \)

\( P( t \leq X \leq s) = \Phi(s) – \Phi(t) \)

Omówienie wzorów wraz z przykładami:

Wiadomości wstępne:

1. \( \Phi(t) = P(X \leq t) \) – dystrybuanta rozkładu normalnego \( X \sim N(0,1) \)
2. Rozkład normalny jest symetryczny, czyli wygląda tak samo względem średniej – w przypadku rozkładu N(0,1) względem x = 0;
3. Prawdopodobieństwo sumuje się do jedynki, tzn. \( P(X \geq a) + P(X < a ) = 1 \)

Przypadki:

1) \( P(X \leq t ) \) gdy \( t \geq 0 \)
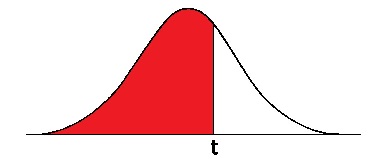Jest to najprostszy przypadek, który możemy od razu odczytać z tablicy:
\( P(X \leq t) =\Phi(t) \)

np. \( P( \leq 2.03 )= \Phi(2.03) \approx 0.979 \)

2) \( P( X \leq t ) \) gdy gdy \( t < 0 \)

3) \( P(X \geq t ) \) gdy \( t > 0 \)

Treść dostępna po zalogowaniu

4) \( P(X \geq t ) \) gdy \( t < 0 \)

Treść dostępna po zalogowaniu

5) \( P( t \leq X \leq s) \)

Treść dostępna po zalogowaniu